Probability Of Getting A Blackjack

You have an awesome sight & I have enjoyed your articles for a few years now... thank you for giving us this web site.
I am been running different numbers thru my head trying to come up with a way to compute the probabilities of getting 3 blackjacks in a row with a 6 deck continuous shuffle machine? Or even the odds of getting 5 blackjacks in a row with the same situation?
Also... I saw a casino promotion where you got a drawing ticket every time you were dealt a red queen and a black ace... is there a way to calculate my odds of getting this type of hand in blackjack?
Thank you
L8lori
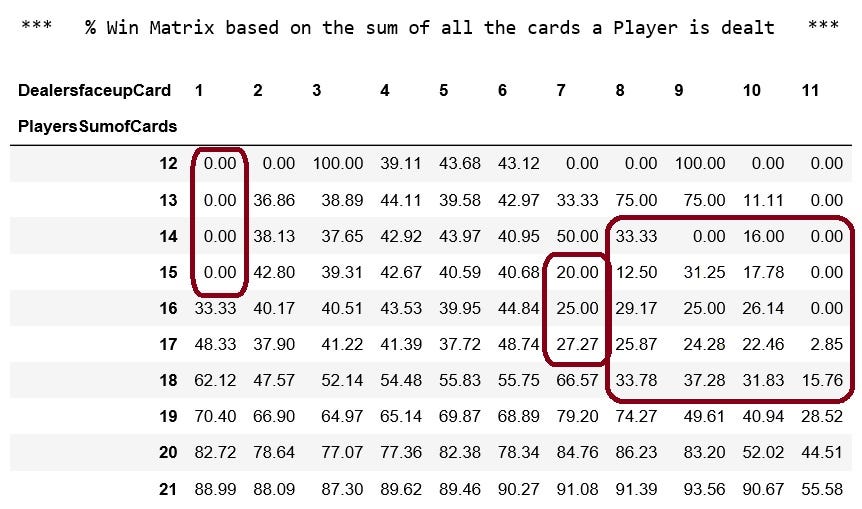
Jun 19, 2014 Assuming that your mom is playing a reasonable strategy, the actual probability is significantly less than this, since in many of the situations enumerated above, she would not draw the third card. The first item on the list, for example, is a blackjack (i.e., total 21) with just the first two cards.
Edit: FYI, from the Wizard's Blackjack page, the general formula for calculating the odds of a blackjack in n decks is: 2*(4/13)*(4n/(52n-1)).
From the Wizard of Odds Blackjack page, the probability of getting a blackjack on a six deck game is: 0.047489. The probability of this happening three times in a row is: (.047489)^3 = .00010709743 or 1 in 9,337
I'm glad it's that low, because I ever actually got three blackjacks in a row, the earth would open up and swallow me and the casino.
I'm glad it's that low, because I ever actually got three blackjacks in a row, the earth would open up and swallow me and the casino.
I got two in a row a few days ago. I was all like 'yay! Blackjack again!'
Calculating Blackjack Probabilities
I think I colored up after that, because I wanted to leave on a high point ;-)I saw a casino promotion where you got a drawing ticket every time you were dealt a red queen and a black ace... is there a way to calculate my odds of getting this type of hand in blackjack?
In a six deck shoe (or CSM) there are 12 red queens and 12 black aces. The odds of getting dealt one of each is (12/312)*(12/311) = .001484 or 1-in-674.
I'm glad it's that low, because I ever actually got three blackjacks in a row, the earth would open up and swallow me and the casino.
1-in-9,337 is not that unusual, when, according to the Wizard, the odds of getting a royal flush in VP, if all you did was try to get a Royal every draw are 1-in-23,081.
In a six deck shoe (or CSM) there are 12 red queens and 12 black aces. The odds of getting dealt one of each is (12/312)*(12/311) = .001484 or 1-in-674.
You neglected that the cards may be dealt in either order, so the probability is twice as great as you calculated.
You neglected that the cards may be dealt in either order, so the probability is twice as great as you calculated.
Thank you for the correction PapaChubby. This is my calculation: (24 (12 red Q's and 12 black A's) / 312 total cards in six decks) * (12 red Q's or black A's, depending on what was dealt first/311) = 1-in-337